Últimamente he estado trabajando en sistemas que requieren de un sistema de balanceo ciego. Esto quiere decir que no conocemos el número de carga soportada en cada sistema, lo hacemos a través de un algoritmo matemático basado en la probabilidad, e incluso parece fácil, muchos lo usan en aplicaciones: cliente para memcached, o como el CEO de Travis-CI. ¿Conocías este sistema?
Para adentrarme de forma rápida, tomaré un poco de información (o inspiración) de los artículos de Tom White y Michael Nielsen en el que se complementa toda la explicación agregando un anillo y la forma matemática del artículo de Math Programming de Jeremy Kun.
Primero vamos a definir lo que es una función hash. Las funciones hash son funciones computacionales que aceptan cadenas de caracteres como entrada y producen números entre 1 y n como salida. En caso de necesitar conocer si un elemento está contenido dentro de un conjunto de elementos, necesitaríamos buscar uno a uno. En conjuntos con gran cantidad de elementos esta acción consumiría una cantidad nada despreciable de tiempo.
El hash permite localizar un elemento x generando un índice h(x) para conseguir su ubicación. Si se elige bien la función de hash se puede minimizar el riesgo de colisiones y aumentar la eficiencia de la función.
Hay muchas formas de generar el hash, hablando específicamente de Erlang tenemos la función erlang:phash/2 y erlang:phash/1-2. Cada función tiene dos parámetros, el término (en Erlang no solo se puede hacer hash de un texto o cadena de caracteres sino también de una estructura de datos) y el rango. En el primer caso el rango se establece entre 1 y el número especificado y en el segundo caso el rango es opcional, en caso de indicarlo se obtiene un número entre 0 y el número menos 1, y en caso de no especificarlo el rango es 2^27.
Se puede observar un ejemplo:
1> erlang:phash(<<"¡hola mundo!">>, 100).
40
2> erlang:phash2(<<"¡hola mundo!">>, 100).
74
3> erlang:phash2(<<"¡hola mundo!">>).
124939106El número está dentro de un rango porque se aplica el módulo del rango elegido sobre el resultado obtenido de realizar la función de hash. Por lo tanto podemos decir que el cálculo sería h(x) mod rango.
Para el caso específico comentado en el título necesitamos conocer el número de elementos entre los que realizar el balanceo. Por ejemplo, si tenemos un clúster de diez servidores podemos crear un balanceador de carga donde se ejecute la función:
erlang:phash(<<"¡hola mundo!">>, 10),El resultado puede emplearse para enrutar hacia un servidor web siempre y cuando se haya asignado un número a cada uno de los servidores disponibles. Si el hash es generado basado en los datos de origen de la petición se puede conseguir que cada petición del mismo origen sea dirigida al mismo servidor web.
El problema con esto es el redimensionado del clúster. Si cambiamos el rango a un número mayor o menor, el resultado para el mismo valor es diferente.
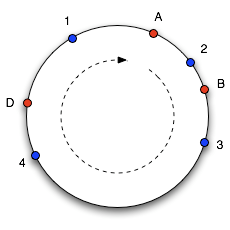
Para resolver este problema se suele pensar en un anillo dividido en un número fijo de trozos. Este número suele ser siempre superior al número de servidores disponibles en cada momento. Por ejemplo, para 10 servidores dividiríamos el anillo en 1000 porciones.
Cada porción del anillo se asigna a un servidor. Cuando un servidor falta, sus asignaciones son repartidas entre el resto. Cuando un nuevo servidor se agrega, se vuelven a repartir todas las particiones.
Esto garantiza un alto grado de concordancia entre peticiones y el servidor al que llegan finalmente, además de un mejor balanceo de la carga entre los servidores, pero no lo garantiza. En los momentos de agregar un nuevo servidor habrá peticiones que vayan al nuevo que antes podrían haber sido asignadas a otro servidor y obviamente en caso de eliminar a un servidor de anillo las peticiones irán a nuevos servidores.
La forma más simple de generar ese anillo (en Erlang) es generar una lista con todos los elementos (los servidores) ordenados y repetidos según el criterio que consideremos oportuno:
% Servidores = [ ... ]
elegir(Peticion, Servidores) ->
Porciones = lists:flatmap(fun(Servidor) ->
lists:duplicate(10, Servidor)
end, Servidores),
N = erlang:phash(Peticion, length(Porciones)),
lists:nth(N, Porciones).Generamos una lista con todas las posibles elecciones para después elegir de esa lista al servidor que atenderá esa petición.
Solo nos falta realizar algunas pruebas para comprobar que todo sea correcto en base a algunas pruebas. Como ejemplo tendré que en lugar de IPs (son más difíciles de generar aleatoriamente) voy a obtener un número aleatorio de números de teléfono en formato internacional:
Telefono = fun() ->
trunc((random:uniform() * 89000000000) + 10000000000)
end.
GenTelefonos = fun(N) -> [ Telefono() || _ <- lists:seq(1,N) ] end.
Telefonos = GenTelefonos(10000).Probaremos con 10 mil números. Los servidores tendrán los siguientes nombres:
Servidores = [
<<"server1">>, <<"server2">>, <<"server3">>, <<"server4">>
].
ObtieneElementos = fun(Servidores, TrozosAnillo) ->
lists:flatmap(fun(Servidor) ->
lists:duplicate(TrozosAnillo, Servidor)
end, Servidores)
end.
Elementos = ObtieneElementos(Servidores, 2048).
Así generamos en Elementos todos los trozos del anillo que necesitamos para la prueba. La haremos con 2048 replicas por servidor, por lo que habrá 2048 x 4 servidores, 8192 trozos en total.
Vamos a definir un par de funciones que simplificarán la generación de las pruebas:
Selecciona = fun(Telefonos, Elementos) ->
lists:map(fun(N) ->
lists:nth(erlang:phash(N, length(Elementos)), Elementos)
end, Telefonos)
end.
Muestra = fun(A) ->
Contadores = lists:foldl(fun(I,D) ->
dict:update_counter(I,1,D)
end, dict:new(), A),
lists:sort(dict:to_list(Contadores))
end.Comenzamos la prueba:
Muestra(Selecciona(Telefonos, Elementos)).
% [{<<"server1">>,2532},
% {<<"server2">>,2503},
% {<<"server3">>,2439},
% {<<"server4">>,2526}]Vemos la salida y elecciones que realiza el código. Hay una varianza de 93 (0,93%) en un total de 10 mil peticiones. Si queremos una mayor precisión solo habrá que incrementar el número de trozos. Además, subiendo el número de peticiones también ayuda a disminuir la varianza. Por ejemplo, con 100 mil:
% en la consola hacemos que olvide Telefonos:
f(Telefonos),
Telefonos = GenTelefonos(100000).
Muestra(Selecciona(Telefonos, Elementos)).
[{<<"server1">>,25189},
{<<"server2">>,24986},
{<<"server3">>,24975},
{<<"server4">>,24850}]En este caso, para 100 mil elementos, la varianza es de 339 (0,34%).
Concluyendo. Este método nos asegura obtener buenos resultados en balanceo de carga sin necesidad de bloquear y controlar las peticiones que tiene cada servidor en cada momento.
¿Has pensado alguna vez en implementar un sistema de balanceo de carga para acceso a cache, servidores web o algún otro recurso? ¿Te interesa conocer más usos y mejoras sobre este tipo de implementaciones? Comenta tu experiencia o pon tus dudas como comentario más abajo.

